
今回は、ブロック線図の等価変換について学習します。
✔学習内容
・よく問われる、頻出のブロック線図の等価変換パターン
・ブロック線図の読み方、記号の意味
・例題(令和元年度技術士一次試験[専門科目] 機械部門 Ⅲ-13)
フィードバック制御などのブロック線図の等価変換に関する問題は技術士一次試験で頻出の問題です。
ポイントを押さえて必ず得点できるようにしておきましょう。
ページコンテンツ
ブロック線図
ブロック線図とは、制御系における信号の伝達を図で示したものです。
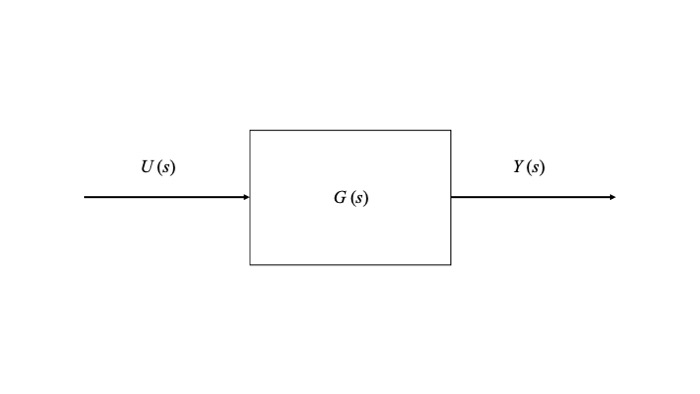
入力$U(s)$、出力$Y(s)$とするとき、伝達関数$G(s)$は、
$$G(s)=\frac{Y(s)}{U(s)}$$
となり、ブロック線図は以下のように表します。
ブロック線図の等価変換
ブロック線図は複数の伝達関数があるとき、等価変換してひとつの制御要素に変形することができます。
以下に覚えておくべき、等価変換のパターンを示します。


以上の等価変換は、技術士一次試験でも頻出ですので受験予定の方は暗記しておくことをおすすめします。
ブロック線図の記号
ブロック線図は矢印や黒丸、白丸、符号などによって構成されています。
- 信号線:信号の経路を矢印で示します。
- 伝達要素:伝達関数をブロックで囲みます。
- 引出し点:黒丸●で示します。1つの信号を分岐して取り出すことを意味します。
- 加え合わせ点(差し引き点):白丸○で示します。2つの信号が足し合わされる(差し引きされる)信号を作りたいときに使います。符号が+の際は、加え合わせます。符号がーの際は差し引かれます。
問題
問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。
【令和元年度技術士一次試験[専門科目] 機械部門 Ⅲ-13】
![令和元年度技術士一次試験[専門科目] 機械部門 Ⅲ-13 問題](https://densya-nazenani.com/wp-content/uploads/2022/03/Professional-Engineer-Exam-R1-13.png)
【解答】
![令和元年度技術士一次試験[専門科目] 機械部門 Ⅲ-13 解答1](https://densya-nazenani.com/wp-content/uploads/2022/03/Professional-Engineer-Exam-R1-13-Ans1.jpeg)
図のように内側の部分を$G_0$として考えます。
すると、系全体の伝達関数は
$$\frac{G_0}{1+G_0\cdot G_3}$$
と表せます。
![令和元年度技術士一次試験[専門科目] 機械部門 Ⅲ-13 解答2](https://densya-nazenani.com/wp-content/uploads/2022/03/Professional-Engineer-Exam-R3-13-Ans2.jpeg)
ここで、$G_0$の中身について、
$$G_0=G_1\cdot\frac{G_2}{1+G_2\cdot G_4}$$
となりますので、代入すると、求める伝達関数は、
$$\frac{G_1\cdot\frac{G_2}{1+G_2\cdot G_4}}{1+G_1\cdot\frac{G_2}{1+G_2\cdot G_4}\cdot G_3}$$
$$=\frac{G_1\cdot G_2}{1+G_2\cdot G_4+G_1\cdot G_2\cdot G_3}$$
よって、正解は④となります。
まとめ

今回は、ブロック線図の等価変換、伝達関数の求め方について学習しました。
直列結合と並列結合、フィードバック結合の等価変換、さらに加え合わせ点と引き出し点の移動の等価変換を暗記して、問題演習を積みましょう。
過去問を完璧に解けるように繰り返し解くことが、技術士一次試験合格の近道です。





















