2自由度振動系の固有角振動数の求め方 【技術士一次試験試験過去問】

本記事では、2自由度振動系の2つの固有角振動数を計算で求めていきます。

自由度

自由度とは、振動系において質点の位置を示すのに必要な変数（変位）の数のことです。

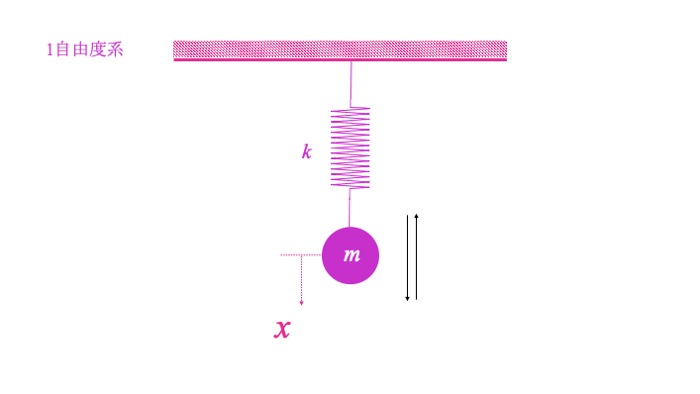
たとえば、図のような系の場合は変位$x$ひとつで質点の位置を表すことができます。

このような振動系を1自由度振動系といいます。

一方、2つの質点がある場合は、$x_1$、$x_2$の2つの変数を使わなければ、位置を表現することができません。

このような振動系を2自由度振動系といいます。

2自由度振動系には2つの固有角振動数が存在します。

問題

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-22】

【解答】

各質点の運動方程式は、

$$\begin{cases}m\ddot{x_1}=-kx_1-k(x_1-x_2)\\m\ddot{x_2}=-kx_2-k(x_2-x_1)\end{cases}$$

$$\begin{cases}{}m\ddot{x_1}=-2kx_1+kx_2\\m\ddot{x_2}=kx_1-2kx_2\end{cases}$$

$x_1=a_1\sin\omega t$, $x_2=a_2\sin\omega t$とすると、連立方程式の上段の式は、

$$-ma_1\omega^2\sin\omega t=-2ka_1\sin\omega t+ka_2\sin\omega t$$

$$-ma_1\omega^2=-2ka_1+ka_2$$

$$a_2=\frac{2k-m\omega^2}{k}a_1$$

とできる。

連立方程式の下段も同様に、

$$-ma_2\omega^2=ka_1-2ka_2$$

とできるので、$a_2=\frac{2k-m\omega^2}{k}a_1$を代入し、

$$-m\frac{2k-m\omega^2}{k}a_1\omega^2=ka_1-2k\frac{2k-m\omega^2}{k}a_1$$

$$-m(2k-m\omega^2)a_1\omega^2=k^2a_1-2k(2k-m\omega^2)a_1$$

$$-m(2k-m\omega^2)\omega^2=k^2-2k(2k-m\omega^2)$$

$$-2mk\omega^2+m^2\omega^4=-3k^2+2mk\omega^2$$

$$m^2\omega^4-4mk\omega^2+3k^2=0$$

解の公式より、

$$\omega^2=\frac{4mk\pm\sqrt{(4mk)^2-4m^2\cdot3k^2}}{2m^2}$$

$$=\frac{4mk\pm\sqrt{16m^2k^2-12m^2k^2}}{2m^2}$$

$$=\frac{4m\pm2m}{2m^2}k$$

$$=\frac{3k}{m}, \frac{k}{m}$$

$$\therefore \omega=\sqrt{\frac{k}{m}}, \sqrt{\frac{3k}{m}}$$

よって、正解は②です。

まとめ

今回は、2自由度系の固有角振動数を求めました。

2自由度系の問題は過去、技術士一次試験に出題されています。

ほかの過去問もぜひ確認してください。