熱伝導と熱伝達の違いは? 【熱力学】

今回は、伝熱について学習します。

伝熱の種類

熱が物体を介して伝わっていくことを「伝熱」といいます。

伝熱には「熱伝導」、「熱伝達」、「熱放射（輻射）」の3つの形態があります。

熱伝導

固体内部や流体内部での熱の移動は一般に「熱伝導」に分類されます。

「熱伝導」では、分子の振動エネルギーが隣接する分子に電波することで熱が伝わっていきます。

基本的に高温側から低温側へ熱が移動していきます。

熱伝達

流体と固体の間での熱の移動は「熱伝達」に分類されます。

例えば、高温の固体があると周囲にある気体（流体）は「熱伝達」によって温度が上昇します。

熱伝達は、流体の対流を生じさせます。

熱放射（輻射）

熱は固体、流体関わらず、真空中であっても電磁波としても熱は伝わります。

熱が電磁波として伝わることは「熱放射」に分類されます。

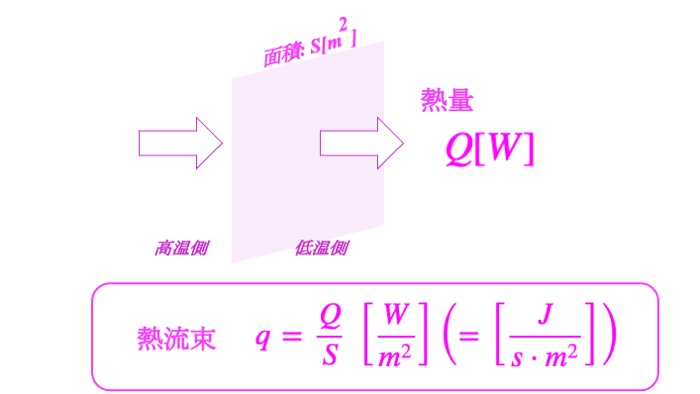
熱流束

熱伝導や熱伝達、熱放射によって、どれだけの熱量が移動したのかを定量するのが「熱流束」です。

単位時間あたりに単位面積を横切る熱量と定義されます。

熱量$Q[W]$が$S[m^2]$を通過したとき、熱流束$q[\frac{W}{m^2}]$は、

$$q=\frac{Q}{S}\space \left[\frac{W}{m^2}\right]\left(=\left[\frac{J}{s\cdot m^2}\right]\right)$$

となります。

以下で熱伝導の場合と熱伝達の場合の熱流束の求め方を説明します。

熱伝導：フーリエの法則

熱伝導による熱流束はフーリエの法則を利用して求めることができます。

フーリエの法則

$$q=-\lambda\cdot\frac{dT}{dx}=\frac{\lambda}{C_p\rho}\cdot\frac{d(C_p\rho)}{dx}$$

• 熱流束: $q\left[\frac{J}{s\cdot m^2}\right]$
• 熱伝導率: $\lambda\left[\frac{J}{s\cdot m\cdot K}\right]$
• 温度勾配: $\frac{dT}{dx} \left[\frac{K}{m}\right]$

熱伝導率は物質によって異なる値をもちます。

熱拡散率

$\frac{\lambda}{C_p\rho}$は「熱拡散率$\alpha$」として用いられることがあります。

熱拡散率

$$\alpha=\frac{\lambda}{C_p\rho}\space \left[\frac{m^2}{s}\right]$$

熱伝達：ニュートンの冷却の法則

固体と流体の間の熱の移動である「熱伝達」の熱流束はニュートンの冷却の法則を利用して求めることができます。

ニュートンの冷却の法則

$$q=h\left(T_w-T_f\right)$$

• 熱流束: $q\left[\frac{J}{s\cdot m^2}\right]$
• 熱伝達率(伝熱係数): $h\left[\frac{J}{s\cdot m^2\cdot K}\right]$
• 固体の温度: $T_w\left[K\right]$
• 流体の温度: $T_f\left[K\right]$

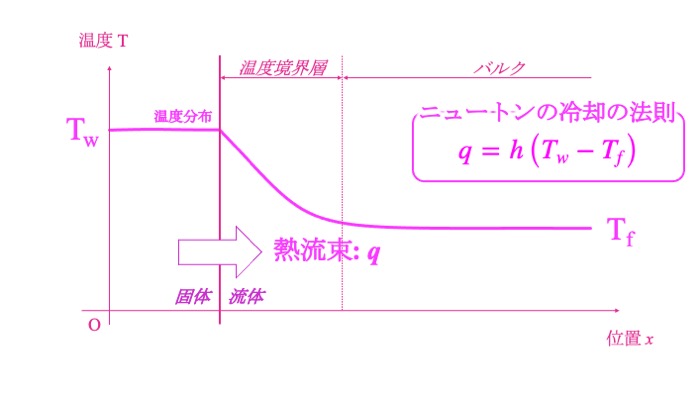
固体と流体の間の熱の移動は温度差に比例します。

熱伝達率は、熱伝導率と異なり物性値ではありません。

固体の表面状態や流体運動によって熱伝達率は変化します。

熱伝達率は、レイノルズ数やプラントル数、グラスホッフ数等の無次元数から求めます。

問題1

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-25】

【解答】

熱流束を$q$とすると、ニュートンの冷却の法則とフーリエの法則により、

$$q=h_1\left(T_1-T_{w1}\right)=\lambda\frac{T_{w1}-T_{w2}}{d}=h_2\left(T_{w2}-T_2\right)$$

よって、以下のように変形できます。

$$\begin{cases}T_1-T_{w1}=\frac{q}{h_1} \\ T_{w1}-T_{w2} = \frac{qd}{\lambda} \\ T_{w2}-T_2=\frac{q}{h_2} \end{cases}$$

未知数である$T_{w1}$、$T_{w2}$を消去すると、

$$T_1-T_2=q\left(\frac{1}{h_1}+\frac{d}{\lambda}+\frac{1}{h_2}\right)$$

$$q=\frac{T_1-T_2}{\frac{1}{h_1}+\frac{d}{\lambda}+\frac{1}{h_2}}$$

ここで、問題文より$\lambda$と$h_2$は、$h_1$と比べて十分大きいとあるので、

$\frac{d}{\lambda}$と$\frac{1}{h_2}$は無視して、

$$q=\frac{T_1-T_2}{\frac{1}{h_1}}$$

$$=h_1\left(T_1-T_2\right)$$

よって、熱通過率として適切なのは⑤です。

問題2

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-27】

【解答】

金属線の水と接している部分の長さを$l$とすると、金属線の発熱量$Q$[W]は、

$$Q=140l$$

ニュートンの冷却の法則より、

$$q=h\cdot\Delta T$$

面積$S$とすると、熱流束$q=\frac{Q}{S}$だから、

$$\frac{Q}{S}=h\Delta T$$

$$Q=h\Delta TS$$

水の温度15℃、金属線の表面温度40℃、金属線の直径は1.5 [mm]だから、

$$140l=h\left(40-15\right)\left\{\frac{1.5}{1000}\pi l+\left(\frac{1.5}{2000}\right)^2 \pi\right\}$$

ここで、$\left(\frac{1.5}{2000}\right)^2\pi$は十分小さいとして無視すると、

$$140l=25\cdot\frac{1.5}{1000}\pi hl$$

$$140=25\cdot\frac{1.5}{1000}\pi h$$

$$h=\frac{140\cdot1000}{25\cdot1.5\pi}$$

$$=1.1889\times10^3$$

よって、最も近い値と思われるのは②です。