周波数伝達関数とは? 実際の求め方を解説! 【制御工学】

今回は、周波数伝達関数の解き方を解説します。

制御工学と聞くと計算が難しい印象をお持ちの方がいると思いますが、ポイントを押さえておくことで楽に計算ができます。

技術士一次試験では避けては通れない分野ですので、しっかり学習してください。

伝達関数とは

伝達関数とは、システムの入出力特性を表す関数です。

システムの微分方程式をラプラス変換することで求めることができます。

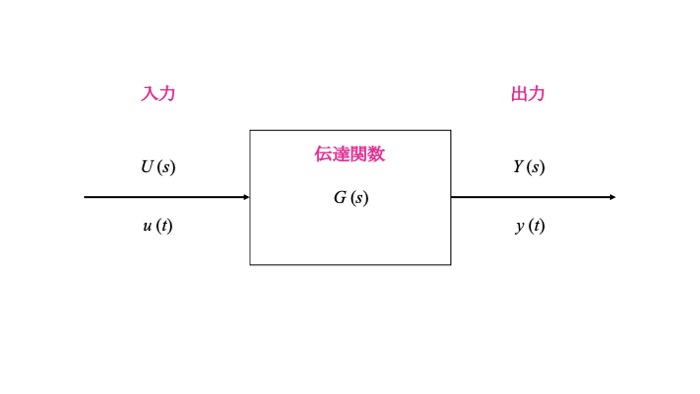
入力$u(t)$をラプラス変換したものを$U(s)$、出力$y(t)$をラプラス変換したものを$Y(s)$とするとき、

伝達関数$G(s)$は以下の式で与えられます。

（すべての初期値はゼロとする：$x(0)=0$）

伝達関数

$$G(s)=\frac{Y(s)}{U(s)}$$

周波数特性とは

入力として、正弦波が使用される場合がよくあります。

$u(t)=\sin \left(\omega t\right)$を入力した場合、$y(t)=A\sin \left(\omega t+\alpha\right)$が出力されます。

ここで、様々な角速度$\omega$の正弦波を入力することによって変化する、出力の振幅比$A$（ゲイン）や位相$\alpha$を調べることにより、システムの伝達関数を知ることができます。

これは未知のシステムの状態を知るのに大変有効な手法で、様々な用途で用いられます。

たとえば、材料の目に見えないレベルの表面状態などを調べるために使用したりされます。

この、出力$y(t)$の入出力振幅比$A$（ゲイン）や位相$\alpha$はシステムのインパルス応答（インパルス入力をシステムに入力したときの応答）をフーリエ変換することで求めることができます。

しかし、この計算は大変面倒です。

そこで、比較的簡単に$A$と$\alpha$を求める手法として、ラプラス変換を用いて周波数伝達関数から求める方法が知られています。

周波数伝達関数

周波数伝達関数とは、システムの伝達関数$G(s)$に$s=j\omega$を代入したものです。

周波数伝達関数: $G(j\omega)$

ここで、$j$は虚数単位を表します。

この周波数伝達関数$G(j\omega)$は実部と虚部からなり、以下のように表現されます。

$$G(j\omega)=a+bj$$

さらに、出力$Y\left(j\omega\right)$は、伝達関数の定義より、

$$Y\left(j\omega\right)=G\left(j\omega\right)\cdot U\left(j\omega\right)$$

とできます。

このとき、入出力振幅比$A$（ゲイン）と位相$\alpha$は以下のようになることが知られています。

・入出力振幅比$A$（ゲイン）

$$A = \sqrt{a^2+b^2}$$

・位相$\alpha$

$$\alpha = \tan^{-1}\left(\frac{b}{a}\right)$$

問題

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-11】

【解答】

入力が正弦波（sin波）であることが確認できます。

また、$u\left(t\right)=\sin t$から、$\omega=1$であることがわかります。

よって、$s=j$を$G\left(s\right)$に代入します。

$$G\left(s\right)=\frac{10}{s+2}$$

$$G\left(j\omega\right)=\frac{10}{j+2}$$

$$=\frac{10\left(j-2\right)}{\left(j+2\right)\left(j-2\right)}$$

$$=4-2j$$

以上から、

$$a=4, b=-2$$

であることがわかります。

入出力振幅比$A$（ゲイン）は、

$$A = \sqrt{a^2+b^2}$$

$$=\sqrt{4^2+\left(-2\right)^2}$$

$$=\sqrt{20}$$

位相$\alpha$は、

$$\alpha = \tan^{-1}\left(\frac{b}{a}\right)$$

$$= \tan^{-1}\left(\frac{-2}{4}\right)$$

$$= \tan^{-1}\left(-\frac{1}{2}\right)$$

よって、出力$y\left(t\right)$は、

$$y\left(t\right)=\sqrt{20}\sin \left(t+\alpha\right),　\alpha=\tan^{-1}\left(-\frac{1}{2}\right)$$

と計算できました。正解は、④となります。

まとめ

伝達関数に関する出題は技術士一次試験において毎年あります。

理解すれば確実に得点できる分野ですので、ぜひチェックして問題演習を積んでください。

過去問を完璧に解けるように繰り返し解くことが、技術士一次試験合格の近道です。