薄肉円筒・薄肉球に働く応力を求める! 【圧力容器】

今回は、薄肉圧力容器に働く応力を求めていきます。

技術士一次試験でも頻出の分野です。

計算結果を暗記することで時間短縮ができるので、導出過程を知り、暗記するのが得策です。

薄肉円筒容器（側面）

円周方向の応力を$\sigma_\theta$とします。

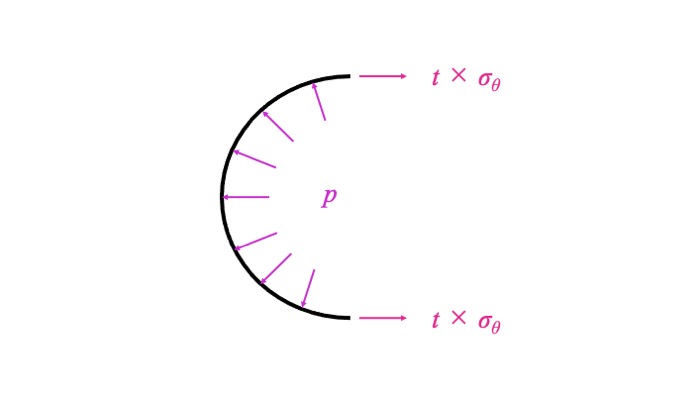
円筒の側面に作用する内圧$p$の合力が、円周方向の力とつりあいます。

$$\int_{0}^{\pi}p\frac{d}{2}\sin\theta d\theta=2t\sigma_\theta$$

$d$: 円筒の直径

$t$: 薄肉の肉厚

この方程式を計算すると、$\sigma_\theta$は、

$$\sigma_\theta=\frac{pd}{4t}\int_{0}^{\pi}\sin\theta d\theta=\frac{pd}{2t}$$

となります。

薄肉円筒圧力容器の円周方向の応力

$$\sigma_\theta=\frac{pd}{2t}$$

薄肉円筒容器（底面）

軸方向の応力を$\sigma_z$とします。

円筒の底面に作用する内圧$p$の合力が、円筒軸方向の力とつりあいます。

$$\pi\left(\frac{d}{2}\right)^2p=\pi dt \sigma_z$$

$d$: 円筒の直径

$t$: 薄肉の肉厚

この方程式を計算すると、$\sigma_z$は、

$$\sigma_z=\frac{pd}{4t}$$

となります。

薄肉円筒圧力容器の軸方向の応力

$$\sigma_z=\frac{pd}{4t}$$

薄肉球殻

薄肉球殻容器に働く応力は次のようになります。

球面方向に作用する応力を$\sigma_\theta$とします。

球の直径が$d$のとき、$\sigma_\theta$は以下のように与えられます。（計算は割愛します）

薄肉球殻容器の応力

$$\sigma_\theta=\frac{pd}{4t}$$

問題

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-10】

【解答】

公式より、薄肉球殻容器の応力は、

$$\sigma_\theta=\frac{pd}{4t}=\frac{pr}{2t}$$

よって、正解は③です。

まとめ

いかがだったでしょうか。

試験では公式を暗記しておくと迷わずにすむでしょう。

球形の$\sigma_\theta$はどこにおいても、円筒における$\sigma_\theta$の半分であり、

材料に付与される応力が小さくすむことがわかります。