強制振動とは? いつ共鳴・共振するか【振動工学】

今回は、強制振動について学習します。

強制振動とは?

強制振動とは、「外部から力を受けることで強制的に生じる振動」のことをいいます。

とくに、外部からsin波やcos波のような周期的な力が加わる際、その周波数が系の固有振動数に近いときに大きな振幅で振動が発生します。

この大きな振動を「共鳴」もしくは「共振」と呼びます。

この共振現象は、小さい地震などであっても被害を大きくすることがあり、建築分野では避ける努力がなされています。

ブランコを押して振動させるのも共振現象のひとつです。

強制振動の運動方程式

それでは、どうして共振現象が生じるのかを計算で確認していきます。

周期的な外力（今回はcos波）が加えられる系の運動方程式は以下の通りです。

$$m\ddot{x}=-kx+F\cos\omega’t$$

• $m$: 質量
• $x$: 変位
• $k$: ばね定数
• $F\cos\omega’t$: 外力（時間$t$によって周期的に変化する）

この方程式を、$\omega_0=\sqrt{\frac{k}{m}}$、$f=\frac{F}{m}$として以下のように変形します。

$$\ddot{x}=-\omega_0^2x+f\cos\omega’t$$

$x=a\cos\omega’t$として、代入すると

$$-a\omega’^2\cos\omega’t=-a\omega_0^2\cos\omega’t+f\cos\omega’t$$

$$a=-\frac{f}{\omega’^2-\omega_0^2}$$

よって、運動方程式の特殊解は

$$x=-\frac{f}{\omega’^2-\omega_0^2}\cos\omega’t$$

となります。

一般解は、

$$x=A\sin\omega_0t+B\cos\omega_0t-\frac{f}{\omega’^2-\omega_0^2}\cos\omega’t$$

となります。

この特殊解をよくみると、$\omega’\approx\omega_0$のときに振幅が非常に大きくなることがわかります。

これが、共振現象の原因です。

共振現象

以下で、共振現象を詳細に考えます。

「外力の周波数が系の固有振動数に近いとき」つまり、

$\omega’\rightarrow\omega_0$の極限を考えます。

初期条件：$x(0)=0, \dot{x}(0)=0$とすると、

$A=0$、$B=\frac{f}{\omega’^2-\omega_0^2}$となるので、

一般解は、

$$x=\frac{f}{\omega’^2-\omega_0^2}\left(\cos\omega_0t-\cos\omega’t\right)$$

和積の公式より、

$$x=-\frac{2f}{(\omega’+\omega_0)(\omega’-\omega_0)}\sin\frac{\omega_0+\omega’}{2}t\sin\frac{\omega_0-\omega’}{2}t$$

$\omega_0-\omega’=\Delta\omega$とすると、

$$x=-\frac{2f}{(\omega’+\omega_0)(-\Delta\omega)}\sin\frac{\omega_0+\omega’}{2}t\sin\frac{\Delta\omega}{2}t$$

$$x=\frac{2f}{\omega’+\omega_0}\sin\frac{\omega_0+\omega’}{2}t\cdot \frac{t}{2}\cdot\frac{\sin\frac{\Delta\omega}{2}t}{\frac{\Delta\omega}{2}t}$$

$\lim_{x \rightarrow 0}\frac{\sin x}{x}=1$より、

極限：$\omega’\rightarrow\omega_0$（$\Delta\omega\rightarrow0$）のとき、

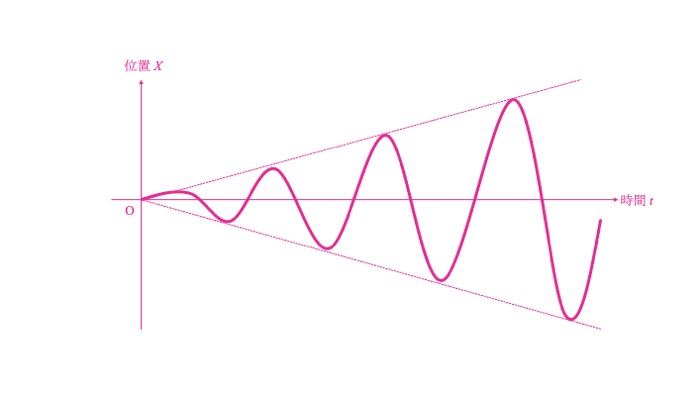
$$x=\frac{ft}{2\omega_0}\sin\omega_0t$$

となります。

この関数は、sinの振幅が時間とともに増大し、以下のようなグラフになります。

まとめ

今回は、強制振動について学習しました。

外力の周波数が系の固有振動数に近いときに共振現象が起こることが理解できたかと思います。

ぜひ、紙に書いて理解してみてください!