
今回は、鉛直ばね振り子の振動について学習します。
✔学習内容
・鉛直ばね振り子の角振動数の求め方
・角振動数$\omega$の意味
・振動数$f$を求める方法
・周期$T$を求める方法
鉛直ばねの角振動数の求め方は他の種類の振動の角振動数を求める際の基本となります。
確実に導出できるようにしておきましょう。
ページコンテンツ
鉛直ばね振り子
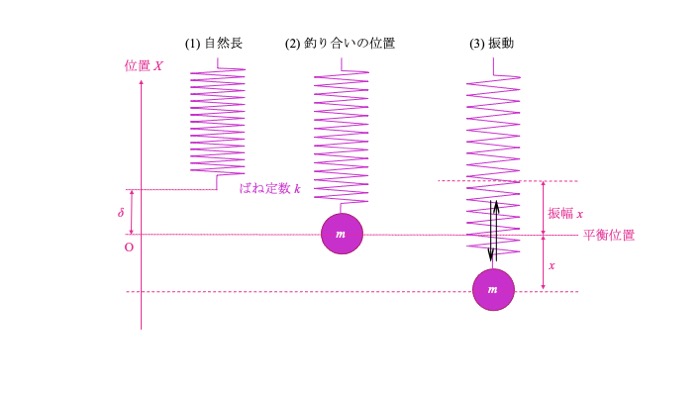
ばねが無荷重の位置((1)自然長)から、質量$m$のおもりを吊るします((2)釣り合いの位置)。
このとき、ばねの引張力とおもりの重力がつりあい、このときのおもりの伸びを$\delta$とします。
力の釣り合いについて、以下の式が成り立ちます。
$$mg-k\delta=0$$
$$mg=k\delta$$
$g$: 重力加速度
$k$: ばね定数
つぎに、振動について考えます。
釣り合いの位置(平衡位置)から、振幅$x$で振動するとすると、運動方程式より次の式が成り立ちます。
$$m\alpha=mg-k\left(x+\delta\right)$$
$$m\alpha=mg-kx-k\delta$$
$\alpha$: 加速度
ここで、(2)にて求めた力の釣り合いの式: $mg=k\delta$より、
$$m\alpha=mg-kx-\color{magenta}{mg}$$
$$m\alpha=-kx$$
加速度は位置$x$を二階微分したものなので、$\alpha$を$\ddot{x}$とおくと、
$$m\ddot{x}=-kx$$
$$\ddot{x}+\frac{k}{m}x=0$$
ここで、$x=A\sin(\omega t+\phi)$とおくと、$\ddot{x}=-\omega^2A\sin(\omega t+\phi)$だから、
$$-\omega^2A\sin(\omega t+\phi)+\frac{k}{m}A\sin(\omega t+\phi)=0$$
$$-\omega^2+\frac{k}{m}=0$$
$$\omega^2=\frac{k}{m}$$
$$\omega=\sqrt{\frac{k}{m}}$$
よって角振動数$\omega$は以下の通りです。
鉛直ばね振り子の角振動数
$$\omega=\sqrt{\frac{k}{m}}$$
角振動数 ω
角振動数$\omega$は、(2)にて求めた力の釣り合いの式: $mg=k\delta$を変形した式($k=\frac{mg}{\delta}$)を用いて以下のように変形できます。
$$\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{\frac{mg}{\delta}}{m}}=\sqrt{\frac{g}{\delta}}$$
角振動数$\omega$は、「ばね定数$k$と質量$m$」もしくは「変位$\delta$」がわかれば求めることができると分かります。
振動数 f
振動数$f$ [Hz]は、以下のようになります。
$$f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$$
周期 T
周期$T$ [s]は、以下のようになります。
$$T=\frac{1}{f}=2\pi\sqrt{\frac{m}{k}}$$
まとめ

いかがだったでしょうか。
自力で導出できるまで紙に書いてみることをおすすめします。
各用語について復習したい方は以下の記事を参考にしてください。























