ばねの合成（直列・並列・サンドイッチ） 【技術士一次試験過去問】

本記事では、ばねの合成について学習していきます。

合成ばね定数

2種類のばねを組み合わせて使用する場合、2つのばねを1つのばねとして考えた時のばね定数を「合成ばね定数」といいます。

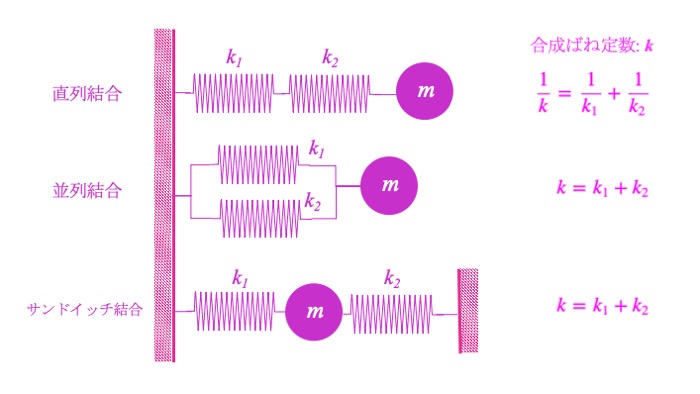
暗記しておくべきばねの組み合わせと合成ばね定数は以下の3つです。

2つのばね定数をそれぞれ$k_1$、$k_2$、合成ばね定数を$k$とすると、

• 直列結合

$$\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}$$

• 並列結合

$$k=k_1+k_2$$

• サンドイッチ結合

$$k=k_1+k_2$$

問題1

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和2年度技術士一次試験[専門科目]　機械部門 Ⅲ-17】

【解答】

合成ばね定数を$K$とすると、

それぞれのばね定数は、

① $k$

② 直列結合だから、

$\frac{1}{K}=\frac{1}{k}+\frac{1}{k}$より、

$K=\frac{1}{2}k$

③ サンドイッチ結合だから、

$K=k+k=2k$

④ 左側は並列結合: $2k$、右側: $k$のサンドイッチ結合で、

$K=2k+k=3k$

⑤ 左側: $k$、右側は直列結合: $\frac{1}{2}k$のサンドイッチ結合だから、

$K=k+\frac{1}{2}k=\frac{3}{2}k$

固有振動数$\omega=\sqrt{\frac{K}{m}}$より、$\omega$が大きくなるのは$K$が大きいときだから、

正解は、④です。

問題2

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-20】

【解答】

ばね定数$k$の2つのばねが並列結合されているので、合成ばね定数$K$は、

$$K=k+k=2k$$

臨界減衰系となるときのダンパの減衰係数（臨界減衰係数）は（導出はこちら）、

$$c=2\sqrt{mK}$$

$K=2k$を代入し、

$$c=2\sqrt{2mk}$$

よって、正解は⑤です。

まとめ

今回は、合成ばねのばね定数について学習しました。

合成ばねの問題は技術士一次試験で頻出です。

過去問を繰り返し解いて合格を目指してください。