縦ひずみと横ひずみ、せん断応力とせん断ひずみとは? 【応力と歪み】

材料の強さなどはそのように評価されるのでしょうか?

材料の強さを調べる方法として、引張試験、圧縮試験など様々な試験方法があります。

これらに代表される試験のように、一般に材料の機械的性質は単軸応力状態にて評価されます。

単軸応力状態とは、一方向のみから力を受けている状態のことをいいます。

今回は、単軸応力状態における材料の変形とその評価に用いる用語について学習します。

変形の種類

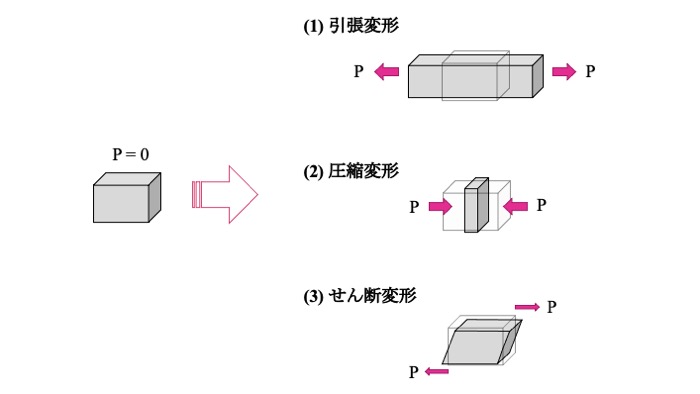
変形の種類は引張変形と圧縮変形、せん断変形の3種類があります。

引張変形と圧縮変形については、こちらの記事で紹介しているので参考にしてうださい。

【応力と歪み】フックの法則とは? 技術士一次試験過去問解説

2022.3.27

応力と歪みの定義を確認します。応力ー歪み曲線を理解し、フックの法則を用いた計算問題を解きます。...

また、公称応力、公称ひずみ、真応力、真ひずみの関係についてはこちらで説明しています。

公称応力、公称ひずみ、真応力、真ひずみの関係! 【応力と歪み】

2022.3.27

今回は、公称応力、公称ひずみ、真応力、真ひずみの関係式を計算します。変形の前後で体積が一定であると仮定するところがポイントとなります。...

縦ひずみと横ひずみ

底面の円の直径$d_0$、高さ$l_0$の円柱を荷重$P$で引っ張り、$d_1$、$l_1$に変形したとします。

このとき、縦ひずみと横ひずみは以下のように定義されます。

• 縦ひずみ　$ε=\frac{l_1-l_0}{l_0}$

• 横ひずみ　$ε’=\frac{d_1-d_0}{d_0}$

この、縦と横のひずみの比は材料によって一定の値となります。この比をポアソン比$\nu$といい、

• ポアソン比　$\nu=-\frac{ε’}{ε}$

と表します。

せん断応力とせん断ひずみ

底面積$A_0$、高さ$h_0$の直方体をせん断方向に荷重$P$を付与し、ひずみ量が$u$であったとき、せん断応力$\tau$とせん断ひずみ$\gamma$は以下のように定義されます。

• せん断応力　$\tau=\frac{u}{A_0}$

• せん断ひずみ　$\gamma=\frac{u}{h}$

せん断応力とせん断ひずみの関係もフックの法則が成り立ちます。

$$\tau=G\cdot\gamma$$

$G$: 剛性率（横弾性係数）[$N/mm^2$]

縦弾性係数（ヤング率）と横弾性係数（剛性率）

ポアソン比$\nu$を使用して、縦弾性係数（ヤング率）$E$と横弾性係数（剛性率）$G$の関係を表すと、以下のようになります。

$$G=\frac{E}{2\left(1+\nu\right)}$$

一般的なポアソン比は$\nu=0.3$程度なので、

$$G=\frac{E}{2\left(1+0.3\right)}$$

$$\approx0.38E$$

よって、せん断応力は引張応力の約40％程度になることがわかります。

まとめ

今回の内容は材料力学を学習するうえで、最も基本となる用語ばかりです。

定義とそれぞれの関係性を押さえておきましょう。