
今回は、振動に関する基本的な用語の意味を確認します。
✔学習内容
・周期$T$、振幅$A$、角振動数$\omega$、振動数$f$の定義
・振動の位置$X$、速度$V$、加速度$\alpha$の関係
振動で使われる用語や単位は普段から使っていなければ、忘れやすいものが多くあります。
不安になったら、この記事に立ち戻って振り返ってください。
ページコンテンツ
周期 T
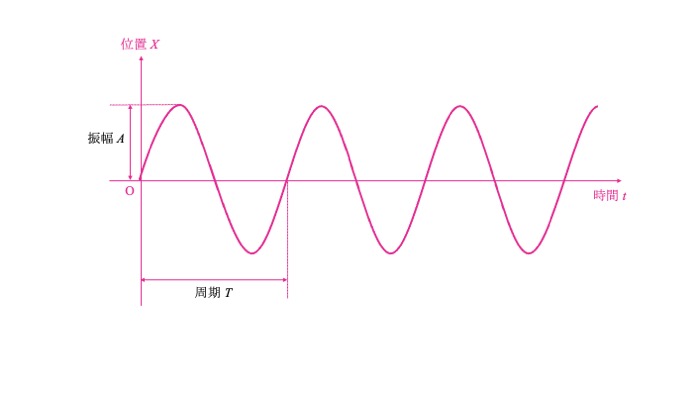
周期$T$ [s]は同じ波が繰り返される振動現象において、波ひとつ当たりの時間です。
振動の変位$X$について、$X=\sin\omega t$とすると、
振動が原点($\omega t=0$)から再び同じ状態に戻る($\omega t=2\pi$)までの時間が周期$T$です。
振幅 A
振幅$A$ [m]は振動の中心から最大変位までの距離のことをいいます。
最小変位から最大変位の距離の半分となります。
角振動数 ω
角振動数$\omega$ [rad/s]はひとつの波につき、単位円を一回転($2\pi$ [rad])すると考えたときの角速度[rad/s]です。
一周($2\pi$ [rad])するのには$T$[s]かかるので、角速度$\omega$は、
$$\omega=\frac{2\pi}{T}$$
となります。
振動数 f
振動数$f$ [Hz]は、単位時間あたりの振動回数です。
単位はヘルツ[Hz]を使います。
振動1回につき、$T$秒かかるので
1秒あたりの振動回数は、周期$T$の逆数となります。
$$f=\frac{1}{T}=\frac{\omega}{2\pi}$$
位置 X
振動の位置$X$ [m]について、基本として正弦波を用います。
$$X=A\sin(\omega t+\phi)$$
状況によっては、他の関数を用いる場合もあります。
速度 V
速度$V$ [m/s]は、位置$V$を時間$t$で微分することにより求まります。
$$V=\frac{dX}{dt}=A\omega\cos(\omega t+\phi)$$
加速度 α
加速度$\alpha$ [m/s2]は、速度$V$を微分することにより求まります。
$$\alpha=\frac{dV}{dt}=\frac{d^2X}{dt^2}=-A\omega^2\sin(\omega t+\phi)$$
まとめ

今回は、振動に関する基本的な用語を確認しました。
冒頭でも述べましたが、振動で使われる用語や単位は普段から使っていなければ、忘れやすいものが多くあります。
また、技術士一次試験では振動工学に関する出題が毎年あります。
問題演習を積む中で不安になったら、この記事に立ち戻って振り返ってください。


![令和3年度 技術士 一次試験 模範解答 [専門科目 機械部門]](https://densya-nazenani.com/wp-content/uploads/2022/02/機械部門解答-300x169.jpg)










![令和3年度 技術士 一次試験 模範解答 [専門科目 機械部門]](https://densya-nazenani.com/wp-content/uploads/2022/02/機械部門解答-150x150.jpg)








