
本記事では、ねじりばねについて解説します。
✔学習内容
・ねじり強さとは
・ねじりばね定数
・例題(令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-16)
ページコンテンツ
ねじり強さ
ある棒を1 [rad]だけねじるのに必要なトルクを「ねじり強さ」と呼びます。
また、「ねじり強さ: $T$」は「ねじりばね定数: $k$」としても使用されます。
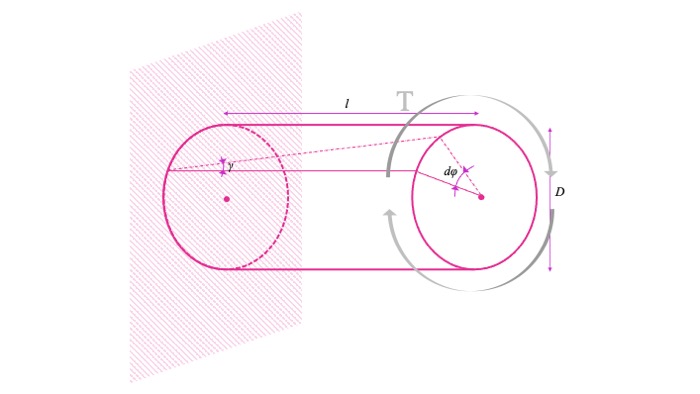
長さ$l$、直径$D$の棒が$\phi$ねじれるとき、比ねじり角$\theta$は、
$$\theta=\frac{d\phi}{dx}=\frac{\phi}{l}=\frac{32T}{\pi GD^4}$$
となります。丸棒のねじれについてはこちらを参考にしてください。
ねじりばね定数$k$は、1 [rad]だけねじるのに必要なトルク$T$なので、
$\phi=1$のとき$T=k$とすると、
$$\frac{\phi}{l}=\frac{32T}{\pi GD^4}$$
$$\frac{1}{l}=\frac{32k}{\pi GD^4}$$
$$k=\frac{\pi GD^4}{32l}$$
と表せます。
ねじりばね定数 $k$[$N{\cdot}m$]
$$k=\frac{\pi GD^4}{32l}$$
$G$: 剛性率
$D$: 丸棒の直径
$l$: 丸棒の長さ
問題
問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。
【令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-16】
![令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-16 問題](https://densya-nazenani.com/wp-content/uploads/2022/03/Professional-Engineer-Exam-R3-16.png)
【解答】
円板について慣性モーメント: $J$より、
$$J\ddot{\theta}=-k\theta$$
$$J\ddot{\theta}+k\theta=0$$
$$\ddot{\theta}+\left(\frac{k}{J}\right)\theta=0$$
この方程式の形から、
$\theta$の係数が$\omega^2$($\omega$: 固有振動数)ですので、(考え方はこちらの記事を参考にしてください)
$$\omega^2=\frac{k}{J}$$
$$\omega=\sqrt{\frac{k}{J}}$$
よって正解は③です。
また、$k=\frac{\pi GD^4}{32l}$ですので、代入し
$$\omega=\sqrt{\frac{k}{J}}=\sqrt{\frac{\pi GD^4}{32lJ}}$$
とできます。
さらに、質量$m$、直径$D$の円板の慣性モーメント$J$は$J=\frac{1}{8}mD^2$ですので、
$$\omega=\sqrt{\frac{\pi GD^4}{32lJ}}=\sqrt{\frac{\pi GD^2}{4lm}}$$
と変形することもできます。
まとめ

今回は、ねじりばねについて学習しました。
振動は様々な問題に触れて慣れることが必要になる分野です。
今回の問題のみならず、参考書や過去問を繰り返し解いてみてください。
技術士一次試験のおすすめ参考書はこちら




![令和3年度 技術士 一次試験 模範解答 [専門科目 機械部門]](https://densya-nazenani.com/wp-content/uploads/2022/02/機械部門解答-300x169.jpg)


















