インパルス応答、ステップ応答、ランプ応答、最終値定理とは? 【フィードバック制御】

今回は、代表的な入力応答であるインパルス応答、ステップ応答、ランプ応答を学習します。

技術士一次試験でも頻出の問題です。

知識があれば解けるものが多いので、最低限暗記すべきところを押さえましょう。

インパルス・ステップ・ランプ応答

最低限覚えておくべき3種類の応答を示します。

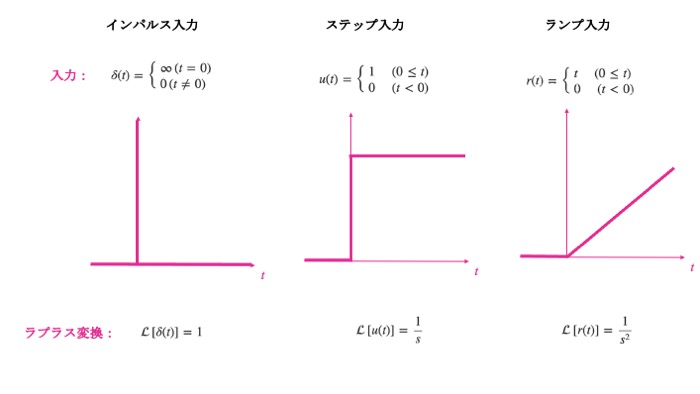
最終値定理

最終値定理は、システムが安定した定常値をだすときその値を求めるための定理です。

時間関数$f(t)$をラプラス変換した関数を$F(s)$とするとき、最終値定理は以下の通りになります。

最終値定理

$$\lim_{t \rightarrow ∞}f(t)=\lim_{s \rightarrow 0}sF(s)$$

問題

問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。

【令和3年度技術士一次試験[専門科目]　機械部門 Ⅲ-14】

【解答】

目標値$r(t)$は、単位ステップ入力とするので、

$$R(s)=\frac{1}{s}$$

となります。

最終値定理より、以下のように変形できます。

$$\lim_{t \rightarrow ∞}e(t)=\lim_{s \rightarrow 0}sE(s)=\lim_{s \rightarrow 0}sR(s)-\lim_{s \rightarrow 0}sH(s)Y(s)$$

ここで、フィードバック系の伝達関数について考えると、

$$\frac{Y(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}$$

$$Y(s)=\frac{G(s)}{1+G(s)H(s)}\cdot R(s)$$

$G(s)H(s)$は問題文で与えられ、$R(s)=\frac{1}{s}$ですので代入できますが、$G(s)$が不明ですので、このままでは$\lim_{t \rightarrow ∞}e(t)$を求めることができません。

よって、以下のように式変形して$\lim_{t \rightarrow ∞}e(t)$を求めることを試みます。

$$E(s)=R(s)-H(s)Y(s)$$
$$=R(s)-H(s)G(s)R(s)$$
$$=\frac{1}{s}-\frac{s+2}{s^3+2s^2+2s+1}\cdot \frac{1}{s}$$
$$=\frac{1}{s}-\frac{s+2}{s(s+1)(s^2+s+1)}$$
$$=\frac{1}{s}-\left(\frac{2}{s}-\frac{1}{s+1}-\frac{s+2}{s^2+s+1}\right)$$

ラプラス逆変換すると、

$$e(t)=-1+e^{-t}+e^{-\frac{1}{2}t}\cos\frac{\sqrt{3}}{2}t+\sqrt{3}e^{-\frac{1}{2}t}\sin\frac{\sqrt{3}}{2}t$$

$$\lim_{t \rightarrow ∞}e(t)=-1$$

となります。

しかし、正解に-1の選択肢はありません。

おそらく、作問者は以下のフィードバック制御、伝達関数を想定して作成したと思われます。

$$\color{red}{\frac{Y(s)}{R(s)}=\frac{G(s)H(s)}{1+G(s)H(s)}}$$

$$\color{red}{E(s)=R(s)-Y(s)}$$

この場合、

$$Y(s)=\frac{G(s)H(s)}{1+G(s)H(s)}\cdot R(s)$$

となります。

最終値定理より、

$$\lim_{t \rightarrow ∞}e(t)=\lim_{s \rightarrow 0}sE(s)$$
$$=\lim_{s \rightarrow 0}sR(s)-\lim_{s \rightarrow 0}sY(s)$$
$$=\lim_{s \rightarrow 0}sR(s)-\lim_{s \rightarrow 0}s\left(\frac{G(s)H(s)}{1+G(s)H(s)}\cdot R(s)\right)$$
$$=\lim_{s \rightarrow 0}s\frac{1}{s}-\lim_{s \rightarrow 0}s\left(\frac{\frac{s+2}{s^3+2s^2+2s+1}}{1+\frac{s+2}{s^3+2s^2+2s+1}}\cdot \frac{1}{s}\right)$$
$$=\lim_{s \rightarrow 0}1-\lim_{s \rightarrow 0}\frac{s+2}{s^3+2s^2+3s+3}$$

$$=1-\frac{2}{3}$$
$$=\frac{1}{3}$$

正解は②となります。

まとめ

技術士一次試験では制御工学に関する出題が毎年あります。

過去問を理解できるまで繰り返し解くことが合格への近道です。

時間を見つけて繰り返し取り組んでみてください。