
今回は、モールの応力円の式を導出していきます。
✔学習内容
・モールの応力円の式を導く
・モールの応力円の読み方
・主応力、主せん断応力の定義
・モールの応力円の書き方
・例題(令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-9)
読むだけでは理解しにくいですので、紙にかいて勉強してみたください!
ページコンテンツ
モールの応力円の導出
2次元において、応力の作用面が$\theta$傾いたとき、垂直応力$\sigma’_{xx}$、せん断応力$\tau’_{xy}$は、
となることは、こちらの記事で説明しました。
この式について以下のように変形し、
2つの式の両辺を2乗して足すと、
となります。これがモールの応力円の式です。
モールの応力円の読み方
モールの応力円
$$\left(\sigma’_{xx}-\frac{\sigma_{xx}+\sigma_{yy}}{2}\right)^2+\tau’^2_{xy}=\left(\frac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau^2_{xy}$$
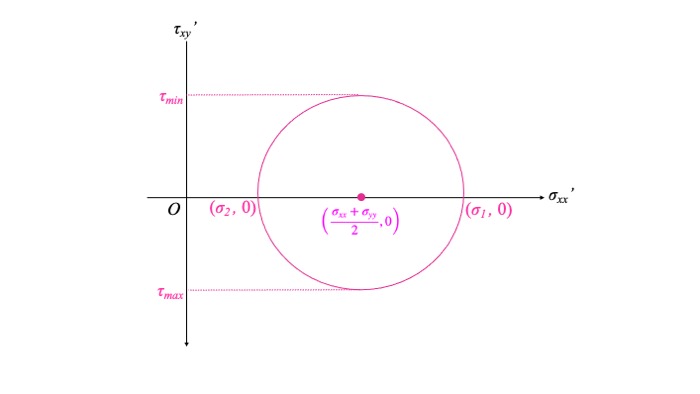
円の中心の座標
円の半径
どのような傾きの作用面であったとしても、垂直応力とせん断応力は必ずこの円上にあります。
主応力
せん断応力がゼロになるとき、垂直応力は最大・最小となります。このような垂直応力を主応力といいます。
主応力はモールの応力円上で、$\sigma_{1}$、$\sigma_{2}$と表されます。
主応力
$$\sigma_{1}=\sigma_{max}=\frac{\sigma_{xx}+\sigma_{yy}}{2}+{\sqrt{\left(\frac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau_{xy}^2}}$$$$\sigma_{2}=\sigma_{min}=\frac{\sigma_{xx}+\sigma_{yy}}{2}-{\sqrt{\left(\frac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau_{xy}^2}}$$
この、最大・最小の垂直応力が作用する面を主応力面といいます。
主応力面
$$\tan2\theta^*=\frac{2\tau_{xy}}{\sigma_{xx}-\sigma_{yy}}$$
主せん断応力
せん断応力が最大となるときのせん断応力を主せん断応力といいます。
この面を主せん断応力面と呼びます。
主せん断応力
$$\tau_{max}=\frac{\sigma_{1}-\sigma_{2}}{2}=\frac{\sigma_{max}-\sigma_{min}}{2}={\sqrt{\left(\frac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau_{xy}^2}}$$
モールの応力円の書き方

モールの応力円を書く際は、引張応力の符号を+、圧縮応力の符号を-で表記します。
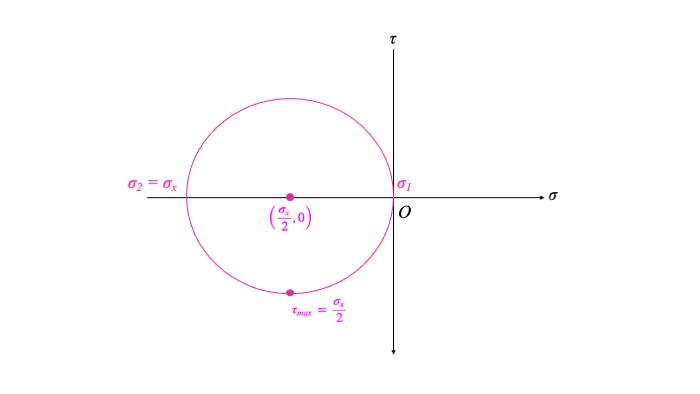
1軸引張応力

【条件】
$\sigma_x=\sigma_x$
$\sigma_y=0$
$\tau_{xy}=0$
モールの応力円はこのようになります。

1軸圧縮応力

【条件】
$\sigma_x=-\sigma_x$
$\sigma_y=0$
$\tau_{xy}=0$
モールの応力円はこのようになります。
2軸応力

【条件】
$\sigma_x=0$
$\sigma_y=\sigma_y$
$\tau_{xy}=0$
モールの応力円は以下のようになります。

純せん断応力

x軸、y軸ともに$\tau_0$のみが作用しているとき、
【条件】
$\sigma_x=0$
$\sigma_y=0$
$\tau_{xy}=\tau_0$
モールの応力円は以下のようになります。

問題
問題画像は公益社団法人日本技術士会ホームページからダウンロードしたものです。
【令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-9】
![令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-9 問題](https://densya-nazenani.com/wp-content/uploads/2022/03/Professional-Engineer-Exam-R3-9.png)
【解答】
ねじりモーメントのみを受ける丸棒の表面は、せん断応力のみを受けることになります。
よって正解は①です。
![令和3年度技術士一次試験[専門科目] 機械部門 Ⅲ-9 解答](https://densya-nazenani.com/wp-content/uploads/2022/03/twisting-moment.jpeg)
ねじりモーメントを受ける丸棒のせん断応力について知りたい方は以下の記事を参考にしてください。
まとめ

いかがだったでしょうか。
試験などで実際に使用する際はモールの応力円の公式を暗記しておくとよいでしょう。




![令和3年度 技術士 一次試験 模範解答 [専門科目 機械部門]](https://densya-nazenani.com/wp-content/uploads/2022/02/機械部門解答-300x169.jpg)


















